В Казани за поправки в Конституцию на 337 участках проголосовали точно так же, как в среднем по России. Вероятность этого — 10 в минус 199-й степени

Во время всероссийского голосования столица Татарстана Казань показала аномальные результаты: на большинстве участков поправки к Конституции поддержали почти ровно 50% зарегистрированных избирателей. «Медуза» оценила вероятность того, что голосование и подсчет бюллетеней были честными.

Что случилось в Казани?

Странное распределение голосов обнаружил блогер Александр Киреев. Из 460 участков для голосования в городе на 337 (по подсчетам «Медузы») 48-52% всех приписанных избирателей проголосовали за поправки. Схожими на этих участках были и явка, и доля бюллетеней с отметкой «за» — 65% и 77% соответственно. Произведение этих двух показателей и дает 50% от списочного числа избирателей. И, что интересно, примерно такие результаты — 67,97% явка, 77,92% «за» поправки от пришедших на участки и 52,95% от всех избирателей — были зафиксированы и на федеральном уровне.

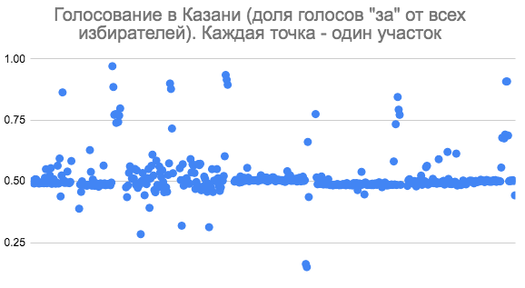
Что в этом странного, раз все так и голосовали?

На самом деле, так мало кто голосовал. В стране было (в основном) два типа участков.

Первый — это кластер с очень высокой явкой и почти 100% голосами «за»; его ученые, много лет занимающиеся исследованием статистики выборов, считают местом, где вбрасывали бюллетени «за» (от этого росла и «явка», и доля «голосующих» за поправки).

Второй кластер с примерно 45% явки и 65% голосов «за» — это участки, где, как считают исследователи, все было честно. Так в среднем и получились общероссийские показатели.

На графике распределение результатов на участках по стране на этом месте находится почти разреженное пространство, где есть только одна большая точка — это 337 участков Казани. Вероятно, одобрение половиной избирателей было нужно организаторам голосования как символический «порог легитимности».

Какова вероятность, что это просто совпадение?

Метод оценки таких совпадений был предложен главным редактором научной газеты «Троицкий вариант», физиком Борисом Штерном после выборов в Госдуму в 2016 году. Тогда он подсчитал вероятность случайного возникновения другой аномалии: на 140 участках в Саратове голоса за «Единую Россию» попали в интервал 62,1-62,3% избирателей.

Штерн предложил сравнить распределение участков внутри и за пределами аномалии. В Саратове внутри «аномалии» в промежутке 62,1-62,3% голосов, подданных за «Единую Россию», оказалось 140 участков, а на таких же по размеру соседних промежутках (61,9-62,1 и 62,3-62,5%) — всего 6 участков. Распределение в 6 участков на 0,2 процентных пункта ученый решил принять за «норму».

Затем Штерн посчитал вероятность аномального «выброса» по сравнению с соседней «нормой» (описывается «распределением Пуассона»); иными словами, была вычислена вероятность того, что вместо ожидаемых «нормальных» 6 участков на 0,2 процентных пункта за «Единую Россию» вдруг могли «честно» распределиться 140 участков. Формулу и обоснование можно посмотреть в статье Штерна. 

В случае с Казанью 2020 года разница в распределении, по подсчетам «Медузы», такая — 337 участков на 4 процентных пункта в «аномалии» и 36 участков на соседние 4 процентных пункта.

Согласно методу Штерна, вероятность того, что «аномалия» в Казани была случайным вариантом честного голосования и подсчета голосов, составляет примерно 10 в минус 199 степени. Вероятность эта столь мала, что, продолжая аналогию Штерна для Саратова, можно заключить: голосование нельзя было бы считать честным с точки зрения статистики, даже если бы оно проходило на каждой планете типа Земли в окрестностях звезды типа Солнца во всей видимой части Вселенной каждый год в течение миллиардов лет. Потому что даже в этом случае ни на одной планете ни в один год не нашлось бы Казани, которая могла бы повторить такое распределение голосов по участкам.